Basics of Graphs

SHORTEST PATH

A person wishing to travel from city A to city B could require the following information.  

1. Is there a path from A to B?
2. If there is more than one path from A to B, which is the shortest?

DIJKSTRA IS A “SINGLE SOURCE ALL DESTINATIONS” ALGORITHM

1. Dijkstra’s algorithm finds the shortest path in a weighted graph containing only positive edge weights from a single source.
2. It uses a priority based dictionary or a queue to select a node / vertex nearest to the source that has not been edge relaxed.
3. Since Dijkstra’s algorithm cannot handle negative edge weights, Bellman-Ford algorithm is used for finding the shortest path in a graph containing negative edge weights

Algorithm: Dijkstra’s Shortest Path 

1. Start with the empty Shortest Path Tree (SPT).
2. Maintain a set SPT[] to keep track to vertices included in SPT.
3. Assign a distance value to all the vertices, (say distance []) and initialize all the distances with +∞ (Infinity) except the source vertex. This will be used to keep track of the distance of vertices from the source vertex. The distance of source vertex to source vertex will be 0.
4. Repeat the following steps until all vertices are processed.
   1. Pick the vertex u which is not in SPT[] and has minimum distance. Here we will loop through the vertices and find the vertex with minimum distance.
   2. Add vertex u to SPT[].
   3. Loop over all the adjacent vertices
   4. For adjacent vertex v, if v is not in SPT[] and distance[v] > distance[u] + edge u-v weight then update distance[v] = distance[u] + edge u-v weight

Let’s consider the graph,

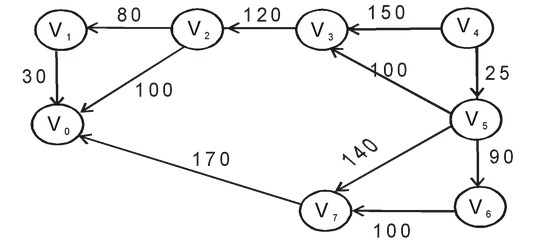
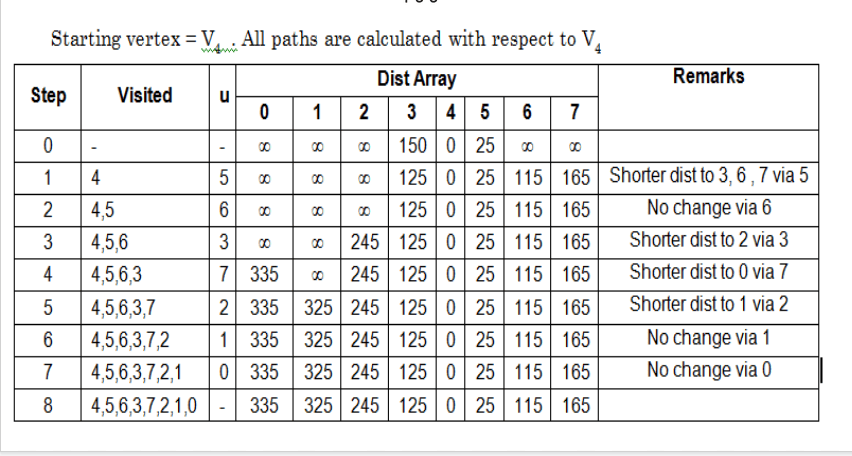
Then Dijkstra algorithm using a matrix results,

void dijkstra(int graph[10][10], int src, int V) 
{ 
	int dist[V];
	bool sptSet[V]; 
	for (int i = 0; i < V; i++) 
		dist[i] = INT_MAX, sptSet[i] = false; 
	dist[src] = 0; 
	for (int count = 0; count < V-1; count++) 
	{ 
	int u = minDistance(dist, sptSet, V); 
	sptSet[u] = true;  
	for (int v = 0; v < V; v++) 
		if (!sptSet[v] && graph[u][v] && dist[u] != INT_MAX 
									&& dist[u]+graph[u][v] < dist[v]) 
			dist[v] = dist[u] + graph[u][v]; 
	} 
	printSolution(dist, V); 
} 

2.Limitation of Dijkstra algorithm:

Dijkstra’s algorithm relies on the fact that the shortest path from s to t goes only through vertices that are closer to s. This is no longer the case for graphs with negative edges, One of the use cases of this is currency cycle with a negative cycle.

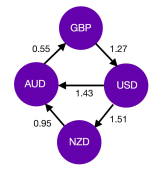
3.Bellman-Ford Algorithm:

Bellman-Ford algorithm finds the shortest path (in terms of distance/cost) from a single source in a directed, weighted graph containing positive and negative edge weights.

Algorithm for Bellman Ford,

1. Initialize the distance from the source node S to all other nodes as infinite (999999999) and to itself as 0.
2. For every node in the graph do
3. For every edge E in the EdgeList do
4. Node_u = E.first, Node_v = E.second
5. Weight_u_v = EdgeWeight ( Node_u, Node_v )
6. If ( Distance [v] > Distance [u] + Weight_u_v )
7. Distance [v] = Distance [u] + Weight_u_v

In a graph with only positive edge weights, Dijkstra’s algorithm with a priority queue / set implementation runs faster in O ((E+V) log V) than Bellman-Ford O (E.V).

TOPOLOGICAL SORT:

AOV network:    A directed graph in which the vertices represent activities or tasks and the edges represent the precedence is called an AOV network. There should be no cycles in an AOV network i.e there should be atleast one activity which does not have a predecessor(start activity). 

Topological sort: If we have an AOV network, then we would like to find out whether the project is feasible or not and if it is feasible, then in what order should the activities be performed so that the project can be completed. The process of converting a set of precedences represented by an AOV network into a linear list in which no later activity precedes an earlier one is called Topological Sorting. This method identifies the order of the activities. 

Let us consider this graph,

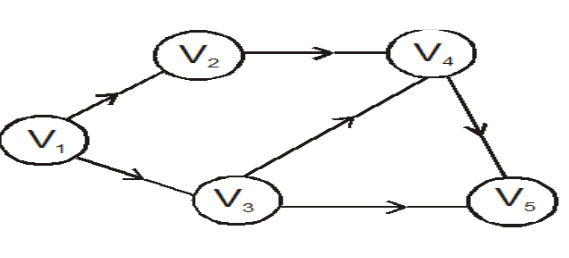
All the steps to perform for topological sort,

The topological order is :V₁, V₃, V₂, V₄, V₅

topologicalSort() 
{ 
	stack<int> Stack; 

	// Mark all the vertices as not visited 
	bool* visited = new bool[V]; 
	for (int i = 0; i < V; i++) 
		visited[i] = false; 

	// Call the recursive helper function to store Topological 
	// Sort starting from all vertices one by one 
	for (int i = 0; i < V; i++) 
		if (visited[i] == false) 
			topologicalSortUtil(i, visited, Stack); 

	// Print contents of stack 
	while (Stack.empty() == false) { 
		cout << Stack.top() << " "; 
		Stack.pop(); 
	} 
} 

Applications of Topological sort:

1. Scheduling jobs from given dependencies among Jobs. F
2. Instruction Scheduling
3. Determining the order of compilation tasks to perform in makefiles, data serializations and resolving symbol dependencies in linkers.

References

1. Research papers of Daniel Kane
2. Research papers from Princeton
3. Research papers from the University of Washington
4. Reference from AlgoTree, Khan Academy and Stackoverflow
5. GitHub repository for code

GitHub repository for code, https://github.com/kakabisht/Data-structures

I have used a lot of images from a lot of sources, and i don’t own images used. I just found them online, and used them to explain concepts. As, images are far better for understanding concepts.