Basics of Graphs

SPANNING TREE:

If G is a graph containing n vertices, then the minimum number of edges needed to connect the n vertices = n-1.  All connected graphs with n-1 edges are trees. These are called spanning trees. 

Definition of Spanning Tree: Let G = (V, E) be an undirected connected graph. A subgraph t = (V, E′) of G is a spanning tree of G iff  t is a tree. 

A minimum spanning tree is a spanning tree with the lowest number of edges. 

MINIMUM COST SPANNING TREE: The spanning tree having the minimum sum of weights of edges is called minimum cost spanning tree. 

These weights may represent the lengths, distances, cost, etc. 

Such trees are widely used in practical applications such as network of road lines between cities, etc. 

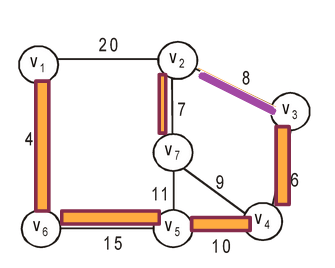
For example.

Algorithms to find minimum spanning tree:

1. PRIM’S ALGORITHM:

A few key points to remember about Prim algorithm,

1. Prim’s algorithm is a greedy algorithm.
2. It finds a minimum spanning tree for a weighted undirected graph.
3. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized.
4. The algorithm operates by building this tree one vertex at a time, from an arbitrary starting vertex, at each step adding the cheapest possible connection from the tree to another vertex.

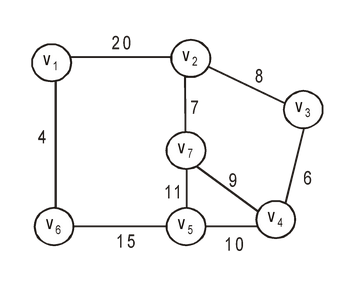
Let’s consider this graph,

All the steps to find Minimum spanning tree using prim’s algorithm,

The end result of minimum spanning tree should look like,

void find_MST(int V)  
    {  
        int parent[V], key[V];
        bool visited[V];

        // Initialize all the arrays 
        for (int i = 0; i< V; i++) { 
            key[i] = 999;    // 99 represents an Infinite value
            visited[i] = false;
            parent[i]=-1;
        }    

        key[0] = 0;  // Include first vertex in MST by setting its key vaue to 0.  
        parent[0] = -1; // First node is always root of MST  

        // The MST will have maximum V-1 vertices  
        for (int x = 0; x < V - 1; x++) 
        {  
            // Finding the minimum key vertex from the 
            //set of vertices not yet included in MST  
            int u = min_Key(key, visited,V);  

            visited[u] = true;  // Add the minimum key vertex to the MST  

            // Update key and parent arrays
            for (int v = 0; v < V; v++)  
            {
                // cost[u][v] is non zero only for adjacent vertices of u  
                // visited[v] is false for vertices not yet included in MST  
                // key[] gets updated only if cost[u][v] is smaller than key[v]  
                if (cost[u][v]!=0 && visited[v] == false && cost[u][v] < key[v])
                {  
                    parent[v] = u;
                    key[v] = cost[u][v];  
                }        
            }
        }

        // print the final MST  
    	print_MST(parent,V);  
    }  

2.KRUSKAL’S ALGORITHM:

A few key points to remember about Kruskal algorithm,

1. Kruskal’s algorithm for finding the Minimum Spanning Tree(MST), which finds an edge of the least possible weight that connects any two trees in the forest
2. It is a greedy algorithm.
3. It finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized.
4. If the graph is not connected, then it finds a minimum spanning forest (a minimum spanning tree for each connected component).
5. Number of edges in MST: V-1 (V – no of vertices in Graph).

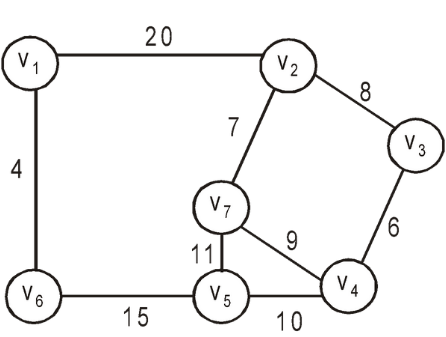
Let’s consider this graph,

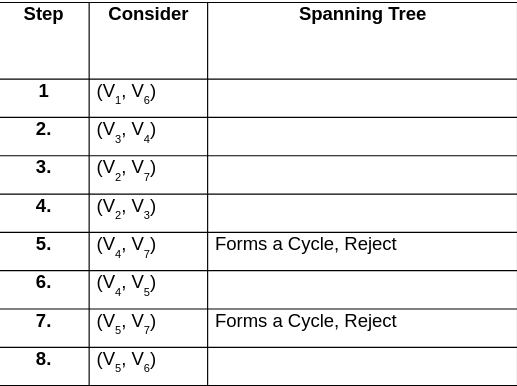
All the steps to find Minimum spanning tree using kruskal’s algorithm,

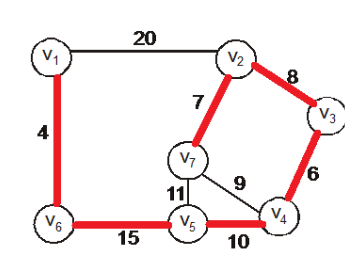
The end result of minimum spanning tree should look like,

void kruskalMST(int V) 
    { 
    	int mincost = 0; // Cost of min MST. 

    	// Initialize sets of disjoint sets. 
    	for (int i = 0; i < V; i++) 
    		parent[i] = i; 

    	// Include minimum weight edges one by one 
    	int edge_count = 0; 
    	while (edge_count < V - 1) { 
    		int min = __INT_MAX__, a = -1, b = -1; 
    		for (int i = 0; i < V; i++) { 
    			for (int j = 0; j < V; j++) { 
    				if (find(i) != find(j) && cost[i][j] < min) { 
    					min = cost[i][j]; 
    					a = i; 
    					b = j; 
    				} 
    			} 
    		} 

    		union1(a, b); 
    		// printf("Edge %d:(%d, %d) cost:%d \n",edge_count++, a, b, min); 
            cout<<"Edge"<<edge_count++<<"("<<a<<","<<b<<")"<<"\t cost:"<<min<<"\n";
    		mincost += min; 
    	} 
    	cout<<"\n Minimum cost="<<mincost<<"\n"; 
    } 

Difference between Kruskal’s and Prim’s Algorithm

Applications of finding minimum spanning tree:

1. Network design
2. Traveling salesman problem